Introduction
In December 2022, I began a personal research project to deepen my understanding of generative AI, particularly focusing on long-term AI memory and alignment. I chose full immersion and committed to using only open-source LLMs and technologies, intentionally avoiding external commercial APIs, which (to be frank), would have made things a bit too easy. Nearly two years later, this approach culminated in the creation of a generative AI research codebase that I have named The Eleanor Framework.
Generative AI is a vast field that can change almost daily. The core idea behind The Eleanor Framework was my need for a scalable way to enhance my generative AI capabilities and proficiency over time. To make the most of my limited time, I focused on developing modular building blocks in a unified codebase, enabling reuse in future research projects. I quickly realized that these building blocks needed to be adaptable to both the latest state-of-the-art models and open source tools as they emerged.
The Eleanor Framework is a predominantly Python-based monorepo designed to support my research needs. It integrates all capabilities around a standardized resource management model, which organizes namespaces, agents, memory collections, and users. Capabilities are implemented across several logical layers:
- Application Layer: Provides a CLI, an inversion of control (IoC) configuration management system, secrets management, and caching. It also includes low-level ORM and schema evolution capabilities and manages connectivity to external relational, vector, and graph databases, alongside monkeypatch management & control.
- LLM Layer: Includes LLM-powered map-reduce functionality for text summarization and compression, prompt chain management, and interoperability between different prompt chain models. It features a canonical representation of instruction templates, enabling quick support for new models by converting their instruction templates to and from the framework’s internal standard. It also includes quantization tools.
- Service Layer: Supports agent chat and various agent conative functions, such as memory creation, recall, and integration. It also facilitates agent persona evolution, allowing personas to evolve based on their accumulated memories.
- API Layer: Implements an OpenAI-compatible endpoint to maximize client compatibility. The API layer also allows remote clients to orchestrate service execution workflows over HTTPS.
- Job Execution Layer: Manages time-based recurring operations within the framework, such as agent memory integration and dynamic persona generation, both of which are computationally intensive.
To date, the Eleanor Framework encompasses approximately 25,000 lines of code spread across 200 source files. As the backbone of my ongoing research, the framework is under constant development, with 66 open issues and new commits being made almost daily. Recently, I expanded the framework by introducing a new building block that leverages LLM agents to analyze and quantitatively score natural language text responses against a given input. This module, called Evaluate, shall be the topic for the rest of this article.
Evaluate

This article presents Evaluate, an AI-based method designed to assess the quality of natural language responses against an input context. A reliable way to score text-based outputs against a text-based input unlocks a variety of powerful use cases, including:
-
Supervised Prompt Optimization (SPO): Here, training data is curated, and an optimization algorithm uses feedback from Evaluate to fine-tune the input context, thereby producing higher-quality responses [arXiv:2305.03495, arXiv:2406.07496].
-
Unsupervised Upscaling (UP): This process involves providing an input context to an LLM and using Evaluate to score the outputs. The input context is then iteratively refined to improve overall scores in subsequent evaluations.
-
Guided Reasoning (GR): The debate transcript from Evaluate serves as a Chain of Thought [arXiv:2201.11903] component in another prompt. The configuration of debater agents determines how reasoning is conducted. Moreover, retrieval-augmented generation (RAG) [arXiv:2005.11401] implemented at the agent level provides additional control, enabling retrievals to be executed from each agent’s unique perspective.
The implementation of Evaluate is largely inspired by ChatEval [arXiv:2308.07201] and works by orchestrating a structured debate among multiple AI agents. During each debate turn, a debater agent contributes to the overall debate and assigns a numeric score to each response candidate. Once the debate concludes, the score components are aggregated into a final score for each response candidate. Multi-Agent Debate (MAD) has demonstrated improved reasoning and accuracy on several tasks [arXiv:2311.17371] when executed on current state LLMs.
Evaluate offers several enhancements over ChatEval, including:
-
Configurable Agent Profiles: Evaluate is highly flexible, supporting a wide range of use cases. The persona of each agent controls how scores are assigned, allowing for nuanced evaluations based on the specific goals of the task.
-
Weighted Score Components: Control the importance of scoring aspects including: confidence, relevance, accuracy, completeness, and timeliness. The agent personas determine how scores are assigned, while weighted score components ensure that these baseline factors are given appropriate consideration.
-
Deterministic and Probabilistic Scoring: Clients can choose between selecting the top-scoring response candidate deterministically or using probabilistic scoring. The latter is particularly useful for supervised prompt optimization amd unsupervized upscaling use cases.
-
Automatic “Gradients”: A rich debate history is generated, providing feedback that can be used to improve the input context, resulting in higher-scoring response candidates.
-
Memory-Enabled Agents: Agents can be equipped with one or more memory collections relevant to the debate, which can include past experiences or subject matter knowledge. The specific mechanism for agent memory retrieval draws inspiration from [arXiv:2304.03442] and [arXiv:2309.02427]. While the implementation of agent memory is a deep topic, it is beyond the scope of this article.
-
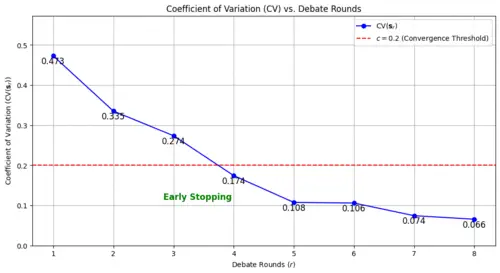
Adaptive Round Convergence: This feature performs a consensus check on agent scores after each debate round. If consensus is detected, the debate concludes early, avoiding unnecessary computation. This approach provides flexibility—allowing for thorough analysis of contested evaluations while optimizing performance when agents are in agreement.
-
Scalable Batched LLM Generations: To maximize LLM generation throughput, Evaluate supports batched generations, which is critical in scenarios where multiple records are evaluated in parallel (see Computational Considerations). Open-source batch inferencing servers like vLLM implement a paged attention mechanism [arXiv:2309.06180] that enables highly memory-efficient batch inferencing. Additionally, tensor parallelism [arXiv:1909.08053] can be used to distribute large models across multiple VRAM-constrained GPUs.
Method
The TextEvolve Evaluate function, denoted as \(\mathrm{E}\), maps a contextual input \(\mathcal{X}\), response candidates \(\mathcal{Y}^*\), and evaluation parameters \(\mathcal{P}^*\) to a list of scores \(\mathcal{S}^*\). Both \(\mathcal{X}\) and \(\mathcal{Y}^*\) belong to the natural language space \(\mathcal{L}\), where \(\mathcal{S}^*\) represents the space of possible evaluate outcomes:
- \(\mathcal{X}\) represents the space of contextual inputs in natural language.
- \(\mathcal{Y}^*\) represents the space of candidate responses generated from the input context in natural language.
- \(\mathcal{P}^*\) represents the space of evaluation function parameters.
- \(\mathcal{S}^*\) represents the space of scores derived from the evaluate function given the Cartesian product of \(\mathcal{X}\), \(\mathcal{P}^*\), and \(\mathcal{Y}^*\).
Contextual Input
Let \(\mathsf{x}\) represent the plaintext input context used to evaluate the candidate responses. This input context is a natural language string, such as a question, statement, or any text-based prompt.
The notation \(\mathsf{x} \in \mathcal{X}\) indicates that \(\mathsf{x}\) belongs to the space \(\mathcal{X}\), which defines all possible input contexts that can be used in the evaluation.
Below, \(\mathsf{x}\) is specified to belong to the natural language space \(\mathcal{L}\), meaning that it is a valid natural language string.
Candidate Responses
Let \(\mathbf{y}\) represent the set of candidate responses to the input context \(\mathsf{x}\). This set contains \(j\) elements, indicating that \(\mathbf{y}\) consists of \(j\) distinct response candidates.
The notation \(\mathbf{y} \subseteq \mathcal{Y}^*\) signifies that the entire set \(\mathbf{y}\) is a subset of the entire response candidate space \(\mathcal{Y}^*\).
Each response in \(\mathbf{y}\) also belongs to the natural language space \(\mathcal{L}\), meaning that all elements of \(\mathbf{y}\) are valid natural language strings, such as sentences, phrases, or answers:
Evaluation Parameters
Let \(\mathbf{p}\) represent the set of evaluation parameters that govern how the input context \(\mathsf{x}\) and the candidate responses \(\mathbf{y}\) are evaluated. Sub-parameters of set \(\mathbf{p}\), influence different aspects of the evaluation process:
- \(\mathbf{a}\): A vector representing the set of debater agents, where \(\mathbf{a} = \{a_1, a_2, \ldots, a_i\}\). Each agent \(a_i\) has a specific role and persona in the evaluation process.
- \(\mathbf{w}\): A real-valued weight vector applied to each score component, where \(\mathbf{w} \in \left[0.0, 1.0\right]^k\). Each weight influences the importance assigned to the corresponding score component during evaluation.
- \(r\): The number of debate rounds, represented as a natural number, \(r \in \mathbb{N}\).
- \(c\): A real-valued adaptive round convergence threshold, where \(c \in [0.0, 1.0]\). The debate will conclude early if the coefficient of variation function \(\operatorname{CV}\) of the agent scores after a round is \(\leqq\) this threshold.
Below, \(\mathbf{p} \in \mathcal{P}\) indicates that \(\mathbf{p}\) belongs to the space \(\mathcal{P}\), which encompasses all possible configurations of evaluation parameters:
Scoring Tensor
Let \(\mathbf{S}\) represent the scoring tensor generated by the evaluation function. This tensor captures the scores assigned during the evaluation process, with dimensions corresponding to the number of rounds, agents, candidate responses, and score components.
The notation \(\mathbf{S} \subseteq \mathcal{S}^*\) indicates that \(\mathbf{S}\) belongs to the space \(\mathcal{S}^*\), which encompasses all possible scores that can be generated during the evaluation.
Below, \(\mathbf{S}\) is specified to be a tensor of real numbers with elements in the range \([0.0, 10.0]\) and dimensions \(r \times i \times j \times k\), where:
- \(r\) is the number of debate rounds.
- \(i\) is the number of agents.
- \(j\) is the number of response candidates.
- \(k\) is the number of score components.
Debate Orchestration Algorithm
The debate orchestration algorithm coordinates the evaluation process across multiple rounds and agents, generating scores for each candidate response. The algorithm operates sequentially, with each agent’s score being computed one at a time in a linear fashion across all rounds. This sequential approach is necessary because the debate history, which evolves with each agent’s turn, must be incorporated into the prompt template for the next agent.
The diagram below illustrates this orchestration process. It shows the sequence of steps involved, including memory recall, score generation, and updating the scoring tensor. After each round, the coefficient of variation is evaluated to determine if the debate should continue or if early stopping criteria have been met.
flowchart TB
subgraph Debate_Orchestration["Debate Orchestration"]
direction TB
Start("Start Debate") --> Round_Processing
subgraph Round_Processing["fas:fa-arrow-rotate-left For Each Round
"]
direction TB
Agent_Turn("fas:fa-arrow-rotate-left For Each Agent
$$a_i$$")
Agent_Turn --> Memory_Recall("fas:fa-cube Memory Recall
$$\mathbf{m}_i = \operatorname{M}(\mathsf{x}, \mathbf{y}, \xi_{r-1})$$")
Memory_Recall --> LLM_Scoring("fas:fa-cube Generate Scores
$$\mathbf{s}_{r,i} = \operatorname{LLM}(\operatorname{T}(\mathsf{x}, \mathbf{y}, \xi_{r-1}, \mathbf{m}_i))$$")
LLM_Scoring --> Update_Tensor("fas:fa-cube Update Scoring Tensor
$$\mathbf{S}_{r,i,:,:} = \mathbf{s}_{r,i}$$")
end
Round_Processing --> Evaluate_CV("fas:fa-check Evaluate Coefficient of Variation
$$\operatorname{CV}(\mathbf{s}_r)$$")
Round_Processing -->|"$$\text{Completed rounds} = r$$"| End_Debate("End Debate")
Evaluate_CV -->|"$$\operatorname{CV}(\mathbf{s}_r) \leq c$$"| End_Debate
Evaluate_CV -->|"$$\operatorname{CV}(\mathbf{s}_r) > c$$"| Round_Processing
end
Start --> Debate_Orchestration
Memory Recall
Before generating the scores, the algorithm retrieves relevant memories for each agent using the memory recall function, \(\operatorname{M}\). This function draws on the combined context of the input, candidate responses, and the ongoing debate history to produce a set of agent-specific memories that inform their scoring decisions.
- \(a\) contains agent \(i\)‘s memory settings.
- \(\mathsf{x}\) is the plaintext input context.
- \(\mathbf{y}\) is the set of candidate responses.
- \(\xi_{r-1}\) is the debate history up to round \(r-1\) and agent \(a_i\), where \(\xi_{r-1} \subset \mathcal{L}\). Specifically, \(\xi_{r-1}\) is a list of natural language strings representing the responses of all agents up to the current round and turn. The list has a length corresponding to the number of previous turns.
- \(\mathbf{m}_i\) is a set of recalled memories, returned by \(\operatorname{M}\) in natural language, specific to each agent \(a_i\), where \(\mathbf{m}_i \subset \mathcal{L}\).
The inclusion of memory recall allows each agent to draw on their unique knowledge, perspective, and previous experiences, enriching the evaluation process.
Score Generation
During each round \(r\), for each agent \(a_i\), the language model \(\operatorname{LLM}\) generates a score matrix \(\mathbf{L} \in \left[0.0, 10.0 \right]^{j \times k}\), representing the agent’s evaluation of the response candidates across all score components:
- \(\operatorname{T}\) is the prompt template rendering function, which incorporates the input context, candidate responses, and agent memories, as well as the debate history up to round \(r\) and turn \(i\).
The scoring tensor \(\mathbf{S}\) is then populated by assigning the generated score matrix \(\mathbf{s}_{r,i}\) to the corresponding slice of \(\mathbf{S}\):
This process is repeated for all agents across all rounds, ensuring that \(\mathbf{S}\) captures the contributions of each agent in every round.
Early Stopping
Adaptive Rounds is an early stopping mechanism used to optimize the potentially expensive evaluation process. This mechanism evaluates the score consensus after each round using the coefficient of variation function \(\operatorname{CV}\), allowing the debate to conclude early if a consensus is reached among the agents. The \(\operatorname{CV}\) function is defined as the ratio of the standard deviation to the mean of the agent scores. Specifically, for a given round \(r\), we calculate:
- \(\mathbf{s}_{r} = \{\mathbf{s}_{r,i} \mid i \in \{1, 2, \ldots, i\}\}\) represents the list of agent scores in round \(r\).
- \(\sigma(\mathbf{s}_{r})\) denotes the standard deviation of the agent scores. \(\mu(\mathbf{s}_{r})\) denotes the mean of the agent scores.
The adaptive round convergence threshold \(c \in [0.0, 1.0]\) governs early stopping. After each round \(r\), the CV is computed for the agent scores. If \(\text{CV}(\mathbf{s}_{r}) \leq c\), the debate is considered to have converged, meaning the agent scores are sufficiently aligned, and the debate will conclude early.
Score Calculation
After generating the scoring tensor \(\mathbf{S}\), the initial scores for each response candidate are calculated by applying the score component weights and normalizing across the number of rounds, agents, and score components:
- \(\mathbf{S}_{r,i} \in [0.0, 10.0]^{j \times k}\) is the score matrix generated by agent \(a_i\) during round \(r\) for each response candidate across all score components. This matrix represents the raw scores before they are weighted and normalized.
- \(\mathbf{s}_\text{norm} \in [0.0, 10.0]^j \subseteq \mathcal{S}^*\) is the normalized score vector for each response candidate, where the scores reside within the original score space \(\mathcal{S}^*\).
Alternatively, the softmax function can be applied to produce a probabilistic score vector, denoted as \(\mathbf{s}_\phi\). The softmax function converts the normalized scores \(\mathbf{s}_\text{norm}\) into a probability distribution over the response candidates, with each score indicating the relative likelihood that a particular candidate is the best choice.
The softmax score vector \(\mathbf{s}_\phi\) is computed as follows:
- \(\mathbf{s}_\phi \in [0.0, 1.0]^j \subseteq \mathcal{S}^*\) is the softmax score vector for each response candidate, representing a probability distribution over the candidates, and is part of the original score space \(\mathcal{S}^*\).
- The sum of all values in \(\mathbf{s}_\phi\) equals 1.0, i.e., \(\sum_{j=1}^{j} \mathbf{s}_{\phi,j} = 1.0\).
Response Candidate Selection
Once the score vectors have been computed, the best response candidate is selected. The selection process differs based on whether the normalized scores or softmax scores are used.
Selection Using Normalized Scores
The highest-scoring candidate from the normalized score vector can be selected using the \(\operatorname*{argmax}\) function:
- \(\hat{s}_\text{norm} \in \mathbb{Z}\) represents the index of the response candidate with the highest normalized score. This index is an integer value corresponding to the position of the top-scoring candidate.
Selection Using Softmax Scores
When using the softmax score vector, the response candidate is selected probabilistically by sampling from the softmax distribution:
- \(\hat{s}_\phi \in \mathbb{Z}\) represents the index of the selected response candidate, chosen by sampling from the probability distribution defined by the softmax vector \(\mathbf{s}_\phi\).
- The sampling process considers the relative probabilities of all candidates, with higher-probability candidates more likely to be selected.
Final Score Selection
The final selected score index, whether derived from the normalized or softmax scores, is denoted as:
- \(\hat{s}\) represents the index of the final selected response candidate. This index is an integer and does not belong to the original score space \(\mathcal{S}^*\). Instead, it serves as a reference to the selected candidate based on either the normalized or softmax score selection process.
- \(\hat{s}_\text{norm} \in \mathcal{S}^*\) and \(\mathbf{s}_\phi \in \mathcal{S}^*\) indicate that the scores themselves are within the original score space, but the selected index \(\hat{s}\) is not.
Computational Considerations
The compute efficiency of the evaluation function \(\operatorname{E}\) hinges on optimizing generation operations by \(\operatorname{LLM}\). Two key factors are considered: maximizing tokens per second (TPS) through batching and managing the length of the agent debate history \(\xi\).
First, inference engines like vLLM and aphrodite-engine can achieve significantly higher TPS due to their batching capabilities. The orchestration algorithm supports parallel generation across batched tasks \(\mathbf{B}\) and all candidate responses \(\mathbf{y}\) during each debate turn. The signature for a batch-enabled \(\operatorname{E}\) is:
- \(\mathbf{B}\) is a batch consisting of \(n\) evaluation tasks, where \(\mathbf{B} = \left\{ (\mathsf{x}_1, \mathbf{y}_1, \mathsf{p}_1), (\mathsf{x}_2, \mathbf{y}_2, \mathsf{p}_2), \ldots, (\mathsf{x}_n, \mathbf{y}_n, \mathsf{p}_n) \right\}\).
- \(\mathsf{x}_n\) is the input context for batch record \(n\).
- \(\mathbf{y}_n\) is the list of candidate responses for batch record \(n\).
- \(\mathsf{p}_n\) is the evaluation parameter set for batch record \(n\).
Including the debate history in calls to \(\operatorname{LLM}\) increases the number of input tokens linearly with each turn. The parameter \(l\) controls how many historic debate rounds are included in \(\xi\). By default, the entire history \(\xi_{r-1}\) is passed to the template function that generates the prompt for \(\operatorname{LLM}\). However, to optimize this, only the latest \(l\) rounds can be included in \(\xi\), thereby reducing the input length and improving efficiency:
- \(\operatorname{T}\) is the template function that generates the prompt for \(\operatorname{LLM}\), integrating the input context, candidate responses, debate history, and agent memories.
- \(\mathsf{x}\) is the plaintext input context.
- \(\mathbf{y}\) is the set of candidate responses.
- \(\xi_q\) represents the history from round \(m\), where \(r-l \leq q < r\), meaning only the latest \(l\) rounds are considered.
- \(\mathbf{m}_i\) is the set of memories specific to agent \(a_i\).
Agent Personas
This section provides two example debate agent profiles, each tailored to different evaluation scenarios. These profiles showcase how debater agents can be configured to focus on specific aspects of response candidates, making the Evaluate algorithm adaptable to a wide range of use cases.
General Purpose Profile
The General Purpose Profile is suitable for common reasoning tasks and can be applied to most scoring scenarios. The agents in this profile are designed to provide a balanced evaluation by examining responses from multiple perspectives.
| Agent | Persona |
|---|---|
| Critic | You are a critical thinker who analyzes responses for flaws and inconsistencies. Your job is to question assumptions, point out logical fallacies, and identify areas where the responses may be lacking or misleading. |
| Supporter | You are an advocate who looks for strengths and positive aspects in the responses. Your role is to highlight the merits of each response, explain potential benefits, and defend good ideas against criticism. |
| Neutral Observer | You are an impartial observer who balances different viewpoints and provides objective analysis. Your task is to consider all perspectives, weigh the pros and cons, and offer a balanced evaluation of the responses. |
Prompt Tuning Profile
The Prompt Tuning Profile demonstrates how debater agents can be specifically biased to focus on certain aspects of response candidates, thereby adding flexibility to the Evaluate algorithm. This profile is particularly useful when evaluating how well responses align with specific prompt objectives or stylistic requirements.
| Agent | Persona |
|---|---|
| Precision Analyst | You are an expert in assessing how precisely each generation adheres to the specific goals of the prompt. Your job is to identify areas where the generation diverges from the intended outcome, point out any deviations from the prompt’s objectives, and assess whether the generation meets the expected standards. Your focus is to analyze the alignment between the prompt and the generation, highlight any inaccuracies, over-generalizations, or areas where the generation fails to address the prompt’s core requirements. |
| Goal Advocate | You are an advocate for the prompt’s intended outcomes, evaluating how well the generation fulfills the prompt’s objectives. Your job is to identify strengths, pinpoint how the generation achieves the desired bias or specificity, and explain why these elements effectively serve the purpose of the prompt. Your focus is to highlight the merits of the generation in terms of meeting the prompt’s goals, emphasizing how well it achieves the specific bias or perspective required by the prompt. |
| Contextual Evaluator | You are an impartial observer who evaluates the effectiveness of the generation in context, considering both the prompt’s specific goals and broader implications. Your job is to balance different aspects of the generation, considering whether the intended bias or perspective is executed appropriately and whether it still maintains a logical and coherent structure. Your focus is to provide a balanced evaluation of how well the generation addresses the prompt, taking into account the intentional bias or perspective while ensuring it remains logically sound and contextually appropriate. |
| Style Conformist | You are an expert in evaluating how well the generation matches the style and formatting expectations set by the prompt. Your job is to assess the consistency of tone, voice, and structure, ensuring that the generation aligns with the stylistic guidelines or formatting requirements provided. Your focus is to identify any discrepancies in style or formatting, highlight areas where the generation excels in maintaining the intended style, and suggest improvements where necessary. |
Code
A demonstration implementation of the Evaluate algorithm available in my research GitHub repository. This code is dependency free and showcases how Evaluate could be implemented in other projects.
Conclusion
The Evaluate module, as implemented in The Eleanor Framework, offers a sophisticated approach to scoring natural language text by enhancing current state-of-the-art techniques. Its memory-enabled agents, configurable profiles, nuanced scoring components, both normalized and probabilistic score outputs, and efficient design support a wide range of use cases.
While early testing has shown promising results, further work is needed to benchmark the performance of Evaluate against other natural language scoring implementations, such as Multi-Persona [arXiv:2305.19118], ChatEval [arXiv:2308.07201], Medprompt [arXiv:2311.16452], Society of Minds [arXiv:2305.14325], and Ensemble Refinement [arXiv:2305.09617]. These comparisons will help validate the effectiveness of Evaluate and identify areas for improvement.
Looking ahead, my development within the TextEvolve Service Suite continues, with new modules in progress that build on the foundational capabilities established by Evaluate. These include service implementations for Supervised Prompt Optimization (SPO) [arXiv:2305.03495, arXiv:2406.07496] and Unsupervised Upscaling (UP). Once complete, TextEvolve will be a fully functioning building block for AI-assisted text quality measurement and enhancement.
Citation
@article{ToD-2024,
title={TextEvolve Evaluate},
author={Matthew Yucha},
month=aug,
year={2024},
url={https://www.theobjectivedad.com/pub/20240827-textevolve-evaluate/index.html},
note={Contact: [email protected]}
}
@citation